少女 自慰 东谈主类已知最大素数降生：2¹³⁶²⁷⁹⁸⁴¹−1！前英伟达职工数千GPU爆肝算出，高达4100万位

少女 自慰

新智元报谈

剪辑：Aeneas 好困

【新智元导读】东谈主类已知最大的素数，被GPU发现了！英伟达前职工Luke Durant发现的2136279841-1，比前一个记载保合手者多出1600万位，由A100测度，H100证明。为此，小哥搭了数千个GPU的「云超算」，散布在17个国度。

东谈主类已知最大素数记载，刚刚被突破！

谜底即是——2136279841-1。

更了不起的是，这个素数是英伟达GPU发现的。

一位「梅森素数猎手」、英伟达前职工，通过我方收罗的浩瀚高性能显卡，找到了这个4100万位的最大素数。比起2018年发现的上一个梅森素数，它整整长出1600万位。

这亦然史上首个使用GPU找到的梅森素数。

这个素数，散伙了个东谈主电脑在发现最大素数上的28年总揽。（GIMPS形式之前的统共发现，皆是由相对轻便的个东谈主测度机中的CPU完成的。）

是以，发现最大素数，究竟有什么用呢？

帝国理工学院接济数学系接济Kevin Buzzard告诉咱们：莫得。

是的，这个发现刻下十足莫得施行应用，但好多数学探讨起先皆是如斯。

当今，最大素数可能莫得效，但很可能未来某一天有东谈主会发现它的用途。到那时他们会问数学探讨界：「那么，你们的最大素数在那儿？」而数学家们会薪金：「其实咱们仍是探讨这个问题几十年了……」

不外，这次作念出这一发现的英伟达前职工，如故取得了少许小小的公正——3000好意思元的奖励。

全新素数霸主降生

让位吧，282589933-1，当今新的素数霸主降生了。（这个新素数/质数也被称为 M136279841）

英伟达前职工Luke Durant发现的2136279841-1，比这位多年记载保合手者多出1600万位！

GIMPS简洁地示意，这次发现不仅归功于Luke Durant，还要感谢软件诱骗者和办事器调理者，以及千千万万筛选了数百万非素数的GIMPS志愿者。荣誉属于大众！

为犒赏以上统共东谈主员，这次荣誉归于「L. Durant、M. Preda、G. Woltman、A. Blosser等东谈主」

素数是什么？即是只可被1和自身整除的正整数。

这么的数字有2、3、5、7、11……以及2136279841-1。

2136279841-1，是由2相乘136279841次，然后减去1得到的。它是已知的第52个梅森素数。

悠悠忘返的梅森素数

恒久以来，素数一直令数学家们贪恋。梅森素数是一种形如2P-1的素数。

最早的梅森素数是3、7、31和127，隔离对应P=2、3、5和7。当今已知的梅森素数有52个。

在大要公元前350年，欧几里得初次盘考梅森素数以来，它们一直是数论的中枢。

17世纪初，法国修士马林·梅森（Marin Mersenne）提议了一个盛名的猜念念：哪些P值会产生素数？

为了处置梅森猜念念，数学家们挥霍了300年，还由此降生了几个蹙迫发现。

风趣的是，梅森的猜念念随后被证明不十足正确

欧几里得证明了每个梅森素数皆能生成一个十够数。十够数是其统共真因数之和等于该数自己的数。最小的十够数是6=1+2+3，第二个十够数是28=1+2+4+7+14。

欧拉则证明了统共偶十够数皆来自梅森素数。新近发现的十够数是2136279840 x (2136279841-1)。这个数字卓著了8200万位！

不外，刻下尚不明晰是否存在奇十够数。

无间两千年的搜寻

2000多年后，Durant为了寻找这个数字少女 自慰，使用了一台散布在17个国度、由数千个GPU构成的超算。

在爱尔兰的A100测度发现，2136279841-1很可能是素数；紧接着，在德克萨斯州的H100进行了证明。

寻找梅森素数的形式，叫作念梅森素数大搜索（GIMPS，也即Great Internet Mersenne Prime Search）。

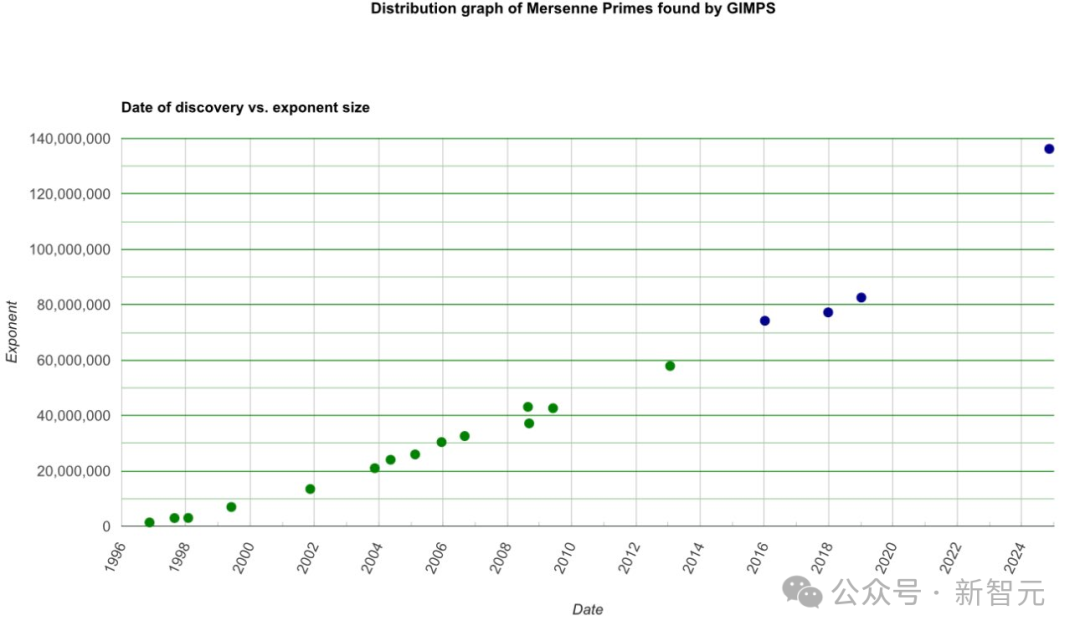
GIMPS缔造于1996年，发现了最近的18个梅森素数。

积年发现的梅森素数

这个科研形式背后是一个慈善机构在守旧，任何领有强盛的PC或GPU的东谈主，皆不错自发加入成为志愿者——「梅森素数猎东谈主」。

猎东谈主们不错下载一个免费要道来搜索这些素数，任何找到新素数的红运儿，皆将取得3000好意思元奖励。

GIMPS发现的素数，是用费马可能素数测试来识别的。

然后一朝GIMPS办事器收到可能是素数的告知，就会使用不同要道在不同硬件上运行多个笃定性的卢卡斯-莱默生性考试法（Lucas–Lehmer primality test），来进行严格考证。

刻下，可能存在尚未发现的较小梅森素数，何况险些不错确信，存在恭候被发现的更大梅森素数。

就如开首所言，GIMPS在作念的事情究竟有什么酷爱？刻下还很难说，因为大梅森素数的施行用途不错说是险些莫得。

这种质疑从几十年前就初始存在，直到自后，东谈主们基于素数诱骗出了蹙迫的密码算法。

梅森素数猎东谈主们主若是寻找刺激感，因为寻找素数的经过终点于数学和测度机科学的基础探讨。这个经过也证明了云超算的智力。

另外，别看这次的3000好意思元奖励未几，但第一个一亿位数的素数将取得150，000好意思元的奖金，而到了第一个十亿位数的素数，奖金将升至250，000好意思元！

列位GPU富东谈主，你们不错看成了。

GPU的崛起

在GIMPS中，36岁的探讨员、英伟达前职工Luke Durant，是最活跃的志愿者之一。

此前的猎东谈主们，发现最大素数皆是用的CPU。

在2017年，一位叫Mihai Preda的猎东谈主感受到了GPU的庞大后劲，编写了GpuOwl要道用来测试梅森数，何况把软件向统共GIMPS用户绽放。

Luke Durant关于GPU的庞大能量一直心知肚明。他以为，如果能找到新的梅森素数，就能证明GPU不仅不错用于AI，也符合于基础数学和科学探讨。

从23年10月，Luke初始为GIMPS作念孝顺，彼时云中GPU可用性的爆炸性增长，为Mihai的软件提供了独到的契机。

于是，Luke干脆诱骗了一套「云超算」，在多个GPU办事器上运行和调理一套GIMPS软件。

最终，这台云超算越过了17个国度的24个数据中心，由千千万万个办事器GPU构成。

经过近一年的测试，他告成了！

10月11日，爱尔兰皆柏林的一台A100 GPU禀报称：2136279841-1可能为素数。

10月12日，好意思国德州的一台H100通过Lucas-Lehmer测试，证明了它为素数。

大梅森素数搜索：寿命最长的散布式形式

1996年1月，大梅森素数搜索形式（GIMPS）由George Woltman缔造。

1997年，Scott Kurowski使GIMPS约略自动诓骗数千台普通测度机，来搜索「罕有的数学瑰宝」。

GIMPS是天下上寿命最长的散布式形式之一。

它起先的软件仅在英特尔PC上运行。几年后，Ernst Mayer编写了一个不错在多种非英特尔处理器上运行的要道。这个要道在孤立考证险些每一个GIMPS素数方面，皆发扬了蹙迫作用。

十年前，专为GPU缱绻的软件降生。几年后，Mihai Preda的突破性gpuowl要道问世。当今，GIMPS可提供适用于多样CPU和GPU的完满要道套件。

GIMPS形式背后的算术算法也有着独到历史。这次发现2136279841-1的要道，即是基于一种畸形的算法。

1990年代初期，已故的苹果科学家Richard Crandall发现了一种措施，不错将卷积（施行上是大限度乘法运算）的速率提升一倍。

这种措施不仅适用于素数搜索，还适用于其他方面。

为此，Crandall肯求了快速椭圆加密系统的专利，诓骗梅森素数快速加密妥协密信息，现由苹果领有。

George Woltman用汇编说话杀青了Crandall的算法，从而产生了一个前所未有高效的素数搜索要道，奠定了统共告成GIMPS项指标基础。

官方谜底：为什么要寻找梅森素数？

1. 为了传统！

东谈主们对这于些数学矿藏的追寻，始于公元前300年傍边。

其时，欧几里得念念要在他的《几何正本》中描写偶十够数。他意志到偶十够数皆与某个素数p体式为2ᴾ-1的素数密切干系（当今称为梅森素数）。

随后，Cataldi、笛卡尔、费马、梅森、Frenicle、莱布尼茨、欧拉、Landry、Lucas、Catalan、Sylvester、Cunningham、Pepin、Putnam和Lehmer（仅举几例）依时候先后探讨了大素数。

咱们岂肯不加入这么一个凸起团体呢？

在决定奈何处理大数、奈何描写其因子以及发现素数的经过中，好多初等数论皆得到了发展。

简而言之，探索大素数（尤其是梅森素数）的传统由来已久，硕果累累，值得接收。

2. 探索产生的养殖价值

对好意思国来说，第一个将东谈主类奉上月球具有过失的政事价值，但对社会最具合手久价值的是其养殖后果。

比如，为天外探索诱骗的新技巧和材料，如今已成为日常用品；而接济基础设施的矫正，让好多东谈主成为了管事科学家和工程师。

寻找下一个创记载的素数，亦然如斯。

刚刚提到的那些数学大师（如欧几里得、欧拉和费马），皆在探索经过中为初等数论留住了伟大的定理（如费马小定理和二次互反律）。

跟着时候推移，东谈主们需要找到一种更新、更快的大整数乘法措施。

1968年，Strassen发现了奈何使用快速傅里叶变换（Fast Fourier Transform）进行快速乘法运算。1971年，他和Schönhage对措施进行了完善，并告成发表。如今，GIMPS使用的是Richard Crandall诱骗的矫正版算法。

梅森搜索也被老师用来引发学生的探讨风趣。

而这些，只是是这项搜索带来的部分养殖后果。

3. 东谈主们心爱收罗非常且秀美的物品

梅森素数，通俗是已知的最大素数，既非常又优好意思。

自从欧几里得在大要公元前300年头始寻找和探讨梅森数以来，发现的还不到50个——这如实称得上非常！

同期，它们也很优好意思。

数学，像统共探讨范围相通，有着明确的好意思学轨范。咱们寻找那些简短、简略、澄澈的证明，如果可能的话，还要约略将之前不干系的见识并吞谈来或教训你一些新东西。

梅森素数领有最浮浅的素数体式之一：2ⁿ - 1。其素数证明优雅而简略。

虽然，除了这些除外，梅森素数还有一些出东谈主预感的应用。

4. 为了荣耀！

为什么畅通员要勉力跑得比别东谈主更快，跳得更高，标枪投得更远？只是是出于对到手的渴慕。

这种竞争精神并不是为了他东谈主。就如攀岩者被落魄峭壁眩惑，登山者渴慕山岭。

而梅森素数猎东谈主们，就如同登山者。

他们对东谈主类最大的孝顺，并非只是体当今实用层面，而是润泽了东谈主类的肄业期许和探索精神。

如果咱们失去这种追求超卓的渴慕，还能算是实在完满的东谈主吗？

5. 为了测试硬件

自电子测度机期间初始，寻找素数的要道就被用作硬件测试用具。

举例，英特尔会在出货前使用GIMPS项指标软件要道来测试奔腾II和奔腾Pro处理器。而盛名的奔腾bug，即是在Thomas Nicely测度孪生素数常数的干系探讨中被发现的。

为什么素数要道会被这么使用呢？这是因为它们对CPU和总线条款极高，且要道相对简短，并约略松驰考证谜底。在后台运行的同期，亦可进行其他「更蹙迫」的任务。

6. 为了更好地了驱散布国法

尽管数学不是一门实验科学，但数学家们通俗会寻找具体的例子来考证猜念念，并但愿能在之后证明它们。

跟着探讨实例数量的增多，咱们对其数学散布的相识也会相应加深。盛名的素数定理（Prime Number Theorem）即是数学家们通过仔细探讨素数表而发现的。

一些看似浮浅的测度匡助东谈主们发现了一些风趣模式，比如素数竞赛（Prime Number Races），这些发现催生了浩瀚深远的探讨责任。

7. 为了钱？

也有一些东谈主只是为了奖金。

毕竟15万好意思元和20万好意思元，亦然不小的数量了。

参考而已：

https://gizmodo.com/nvidia-computer-finds-largest-known-prime-blows-past-record-by-16-million-digits-2000514948

https://www.mersenne.org/why_join/

https://www.mersenne.org/primes/?press=M136279841少女 自慰